马上注册,结交更多好友,享用更多功能,让你轻松玩转社区。
您需要 登录 才可以下载或查看,没有账号?立即注册
×
就好像掷硬币,两个面出现的几率是各百分之五十,可结果却不是这样,就像赌博就输和赢就是百分之五十的几率,可为什么到最后输的是多数人,赢的却寥寥无几那?你百思不得其解,明明是公平的50%赢面,在50%概率下至少不会亏本的,可为什么最后会输光?
你看的见的是概率,看不见的是陷阱,50%的几率你也会输光,这个陷阱就是:大数定律。
普通人以为的公平,是对大数定律的误解然而,正是这种你以为的“公平”,才陷入了“赌徒谬论”里呢? 先来看看这种让你觉得“公平”的大数定律究竟是什么。
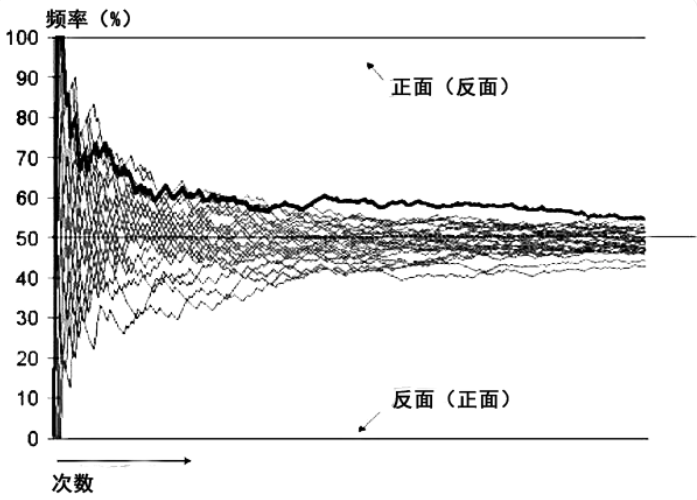
以掷硬币为例,当投掷次数足够多时,出现正(反)面的频率将逐渐接近于1/2,且随着投掷次数的增加,偏差会越来越小,这是大数定律。 但是多少次是足够多?确实没有人知道。50%是统计的平均值,却不是实际分布值,这就是你对大数定律的误解之一。
即下一把就可以赢回来的强烈错觉,大数定律有一个明显的潜台词: 当随机事件发生的次数足够多时,发生的频率便趋近于预期的概率。但人们常常错误地理解为:随机意味着均匀。 如果过去一段时间内发生的事件不均匀,大家就会“人工”地从心理上把未来的事情“抹平”。也就是,如果输了第一把,那下一把的赢面就会更大。这就是你的误解之二。
而且庄家不是赌徒,庄家只靠抽水赚钱,他赚的钱之和你的赌注大小有关
最终的答案是: 论理性,没有人能比赌场老板更理性。 论数学,没有人能比赌场老板请的专家更精通数学。 论赌本,没有人能比赌场老板的本钱更多。
|